영상 기반의 움직이는 객체의 검출 및 추적은 실시간 감시 시스템이나 영상회의 시스템 등에서 널리 사용되고 있다. 또한 인간-컴퓨터 상호 작용(Human-Computer Interface)이나 인간-로봇 상호 작용(Human-Robot Interface)으로 확장되어 사용할 수 있기 때문에 움직이는 객체의 추적 기술은 중요한 핵심 기술 중에 하나이다. 특히 다중 객체의 움직임 환경에서 특정 객체의 움직임만을 추적할 수 있다면 다양한 응용이 가능할 것이다. 본 고에서는 파티클 필터를 이용한 특정 객체의 움직임 추적에 관하여 연구하였다. 실험 결과들로부터 파티클 필터를 이용한 단일 객체의 움직임 추적과 다중 객체의 움직임 환경에서 특정 객체의 움직임 추적방법에 관한 좋은결과를 얻을 수 있었다.
                                                                                                                                                                                                                                                               심귀보 교수                                                           김형복
kbsim@cau.ac.kr 
                                                                           중앙대학교 전자전기공학
중앙대학교 전자전기공학부

영상 기반의 움직이는 객체의 검출 및 추적은 실시간 감시 시스템이나 영상회의 시스템 등에서 널리 사용되고 있다. 실시간 감시 시스템의 경우 움직이는 객체가 많지 않은 환경에서 객체의 움직임을 자동으로 감지하고 이를 추적함으로써 인간의 역할을 대신할 수 있는 컴퓨터 비전 시스템에 응용되고 있으며, 영상회의 시스템의 경우에는 화자 또는 특정 인물의 움직임을 판단하고 이를 추적하는 실시간 영상회의 시스템에 응용되고 있다. 또한 인간-컴퓨터 상호 작용(Human-Computer Interface)이나 인간-로봇 상호 작용(Human-Robot Interface)으로 확장되어 사용할 수 있기 때문에 움직이는 객체의 추적 기술은 중요한 핵심 기술 중에 하나이다. 일반적으로 영상 기반의 움직이는 객체의 추적은 실시간으로 변화하는 이미지 스트림을 이용한다. 각각의 프레임에서 객체의 움직임을 추적하기 위해서는 연속되는 비디오 영상의 프레임 분석과 실시간 모니터링, 움직이는 객체의 순간적인 변화의 예측이 요구되어지며, 프레임에 대한 분석을 통하여 추적 대상을 검출하고 위치 변화를 계산하여 이동 객체의 이동방향, 속도 등의 정보를 추출하게 된다. 영상에서 객체의 움직임 정보를 추출하는 방법 중 가장 널리 사용하는 방법은 옵티컬 플로우(Optical flow)와 블록 매칭 알고리즘(Block matching algorithm) 등이 있다. 옵티컬 플로우는 많은 계산량을 필요로 하기 때문에 실시간 처리에는 적당하지 않다. 또한 영상의 압축에 사용하는 움직임 예측 방법 중 하나인 블록 매칭 알고리즘은 실시간으로 영상 내 객체의 움직임 벡터(Motion vector)를 추출하여 객체를 추적하는 방법이지만 다중 객체가 움직이는 환경에서는 객체의 움직임 추적이 불가능하다는 문제점이 있다.이동 물체 추적에 있어서 실제 이동 물체 추적 시스템에서 주로 쓰이는 추적 필터는 칼만 필터(Kalman filter)가 있는데 이는 선형/가우시안 잡음 시스템에서 최적으로 알려져 있다. 칼만 필터는 상태 변수 추정을 위한 사후 분포가 해석적으로 구할 수 있다는 장점이 있다. 하지만 실제 시스템이 비선형이거나 부가되는 잡음이 가우시안이 아닐 경우 칼만 필터처럼 사후 분포를 해석적으로 구하기가 어려워진다. 이러한 선형 시스템의 칼만 필터와 달리 비선형 시스템에 대해서는 아직까지 최적 필터가 존재하지 않으며 다양한 준 최적 필터는 존재한다. 대표적인 필터로는 시스템 모델에 강제적인 선형화를 요구하는 EKF(extended Kalman filter), 다중 모델 필터, 샘플링 이론으로 접근한 필터 등이 존재한다.하지만 최근에 컴퓨터의 연산 처리속도와 처리량이 급격히 증가하게 되면서 비선형 시스템 추정에 있어서 샘플링 이론으로 접근한 UKF(unscented Kalman filter), 파티클 필터(Particle filter) 등이 활발하게 연구되고 있다. 이 중 파티클 필터는 대표적인 추적 필터인 칼만 필터와 달리 사후 분포를 해석적으로 구하는 것이 아니라 상태 변수를 대표할 수 있는 다수의 파티클과 각 파티클이 가지는 가중치(weight)를 통하여 표현하고 있다. 최근 파티클 필터에 의한 이동 객체 추적 방법이 복잡한 환경 속에서 움직이는 객체를 추적하는데 효과적이라고 알려져 있으며, 현재 이동 객체 추적 분야에서 가장 이슈가 되고 많이 쓰이고 있는 이론이다.따라서 본 고에서는 객체 추적에 많이 사용되고 있는 블록 매칭 알고리즘을 이용한 객체의 움직임 추적 방법에 대해 설명하고 문제점에 대해서 생각해 본 후, 본 고에서 제안하는 파티클 필터를 이용한 다중 객체의 움직임 환경에서 특정 객체의 움직임 추적 방법에 대해서 설명하고자 한다.블록 매칭 알고리즘
  식 (1)에서  SAD값을 가장 작게 만드는 변위 (u,v)의 값이 해당 블록의 움직임 벡터이다. SAD(x,y)(u,v)의 최소값을 갖는 움직임 벡터 (u,v)를 v(u＾+v＾)로 나타내면 식(2)와 같다.검색 윈도우 안에서 해당 블록과  SAD값이 가장 작은 위치의 블록을 찾고, 그 위치 변화를 움직임 벡터로 인지하게 된다. 그림 1은 블록 매칭 알고리즘의 움직임 추정 과정을 보여주고 있으며, 그림 2는  SAD를 이용한 움직임 벡터 검출 결과를 보여주고 있다. Current Frame(t)에 존재하는 M×N크기의 블록이 Previous Frame(t-1)의 어느 위치에 해당하는지의 여부를 원도우를 통해 검색을 한다. 이 검색 원도우 안에서 해당 블록과  SAD값이 가장 작은 위치를 블록으로 찾고, 그 위치 변화를 움직임 벡터로 추출 한다.블록매칭 알고리즘에서 움직임 추정 방법에는 Cross Search, Full Search, Spiral Search, Three Step Search가 있다. 본 고에서는 특정 블록 주변의 모든 변위에 대하여 SAD를 계산 하는 방법인 Full Search방법을 이용하여 Motion Vector를 추출한다. Full Search를 사용하면 가장 정확한 블록 매칭 기반 Motion Vector을 알아낼 수 있다. 그러나 원도우의 크기가  커질수록 Full Search 방법은 너무 많은 연산 시간을 필요로 하는 단점이 있다. 이러한 단점을 보완하기 위해 일부 위치에 대해서만 SAD를 계산하는 방법들이 개발되었다. 다이아몬드 검색(Diamond Search) 방법은 빠르고 정확한 움직임 추정 방법의 하나로 알려져 있다.블록 매칭 알고리즘을 이용한 실험 결과

본 고에서의 모든 실험은 Microsoft Visual studio 2008을 사용하여 표 1에 보이는 사양의 PC를 사용하였다.그림 3과 그림 4는 블록 매칭 알고리즘을 이용한 단일 객체의 움직임 추적 결과이다. 그림 3의 실험은 컴퓨터 시뮬레이션 동영상을 사용하여 실험 하였으며, 매우 작은 객체의 움직임 추적에 대한 실험이다. 그림 4의 실험은 일본 혼다의 아시모(ASIMO) 로봇이 뛰는 동영상을 사용하여 실험을 하였으며, 비교적 큰 객체의 움직임 추적에 대한 실험이다.

실험 결과로부터 크기가 큰 객체의 경우는 비교적 객체의 움직임을 잘 추적하는 것을 볼 수 있지만, 크기가 작은 객체의 경우는 객체의 움직임을 추적하지 못하는 것을 볼 수 있다. 이러한 문제를 해결하는 방법은 블록의 크기를 더욱 작게 하는 것이다. 그러나 블록 매칭 알고리즘은 객체의 움직임이 한 블록 내에서 모두 동일하다고 가정하는데, 블록의 크기가 작을수록 이러한 가정의 신뢰도는 높아지나 움직임 벡터의 계산량과 전송량이 증가하게 된다.
 파티클 필터(Particle Filter)

파티클 필터(Particle Filter)는 객체 추적에 있어서 최근 들어 가장 널리 사용되고 있는 알고리즘이다. 파티클 필터는 시뮬레이션에 기반을 둔 예측 기술의 하나로 SMC(Sequential Monte Carlo) 방법이라고도 하며, non-Linear, non-Gaussian 시스템에 적합한 알고리즘이다. 파티클 필터의 목적은 연속적으로 들어오는 정보를 오차가 존재하는 관측 값만을 가지고 정보를 예측하는데 있다.

파티클 필터의 동작 원리는 매우 간단하다. 시스템에 적절하게 제안된 확률분포로 임의로 생성된 입력을 여럿 가하여보고 그것들을 종합하여 시스템의 정보를 추측하는 것이다. 베이지안 필터링(Bayesian filtering) 방법과 같이, 파티클 필터는 식 (3)을 반복하여 사용하는 마르코프 과정(Markov process)의 사후확률(Posterior probability)을 관측한다.식 (3)에서 각각의 수식이 나타내는 의미는 다음과 같다.
 Xt  : the unobserved state or process state at time
 Yt  : the observation at time
 Y1:t   : the sequence of observation from 1 to
 p(Xt│Xt-1) : the state motion model or the process dynamical distribution
 p(Yt│Xt)  : the observation model or the observation likelihood distribution
 α  : a normalizing factor or a normalizing constant
 P(Xt│Y1:t) : current object state or posterior distribution
 P(Xt-1│Y1 : previous object state식 (3)의 integral은 기본적인 경우를 제외하고 closed form solution을 가지지 않는다.
따라서 식 (3)은 weighted samples(particles)의 집합  {(Xt(i),wt(i))}i=1,...,N을 이용하여 근사화하여 사용한다. 여기서 Xt(i)는 파티클을 나타내며, wt(i)는 각 파티클에 대응되는 가중치(weight)를 나타낸다. Current object state P(Xt│Y1:t)를 파티클 Xt(i)와 가중치 wt(i)로 나타내면 식 (4)와 같다. 식 (4)에서 δ는 Dirac delta function을 의미한다.식 (4)를 Previous object state P(Xt-1│Y1:t-1)에 관한 식으로 변경한 후, 변경한 식을 식 (3)에 대입한 후 정리하면 식 (5)를 얻을 수 있다.식 (5)의 filtering distribution을 유지하기 위해,  N개의 파티클 집합은 이전 시간 단계에서의 filtering distribution을 나타낸다는 사실을 가정한다. 즉, p(Xt-1│Y1:t-1)쩁{(Xt(i)-1,wt(i)-1)}i=1,...,N이다. 새로운 N개의 파티클 집합 Xt(i)i=1,...,N은 proposal distribution Xt(i)∼q(Xt│X0:t-1,Y1:t)로부터 샘플되어지고, 이 파티클 집합에 대한 importance weights는 식 (6)에 따라 계산되어진다.파티클 필터의 마지막 단계로써, 파티클은 그들의 importance weights에 비례해서 Resampling 과정을 거치게 된다. 실험에 사용한 파티클 필터 모델

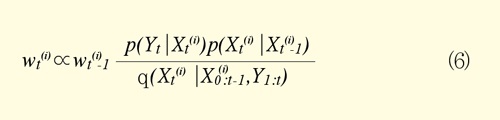
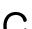
앞의 내용으로부터 파티클 필터를 사용하기 위해서는 기본적으로 3가지를 정해 주어야 한다.(1) Initial state : Est(0)=p(X0)본 고의 실험에서는 추적하고자 하는 객체의 영역을 마우스 입력을 통해서 초기화하였다.(2) State motion model : p(Xt│Xt-1)
본 고의 실험에서는 추적하고자 하는 객체 Xt를 전체 프레임 영역에서의 사각형 영역(Xt={x,y,width, height})으로 정의한다. 본 고에서는 현재 객체의 위치를 평균으로 하는 가우시안 분포(N(μ,Σ))를 통해 파티클 (Xt(i))들을 생성한다. 즉, Xt(i)∼N(position of Xt-1,Σ)이다.(3) Observation model :  p(Yt│Xt)본 고에서는 HSV 색상 기반의 히스토그램(Histogram)을 이용한다. HSV 색 공간은 색상(Hue), 채도(Saturation), 명도(Value)의 좌표를 사용하여 특정한 색을 지정하는 방법이다. 일반적으로 HSV 색상 기반의 히스토그램을 사용한 실험이 RGB 색상 기반의 히스토그램을 사용한 실험보다 더 좋은 성능을 보인다.
본 고에서 추적하고자 하는 객체의 히스토그램과 파티클 각각의 히스토그램과의 비교를 통해 추적하는 객체의 다음 위치를 정하게 된다.파티클 필터를 이용한 실험 결과

그림 5와 그림 6은 파티클 필터를 이용한 단일 객체의 움직임 추적 결과이다. 그림 5의 실험은 그림 3에서 사용한 컴퓨터 시뮬레이션 동영상을 사용하여 실험을 하였으며, 매우 작은 객체의 움직임 추적에 대한 실험이다. 또한 6의 실험은 그림 4에서 사용한 일본 혼다의 아시모(ASIMO) 로봇이 뛰는 동영상을 사용하여 실험을 하였으며, 비교적 큰 객체의 움직임 추적에 대한 실험이다. 그림 5와 그림 6의 실험 결과로부터 객체의 크기와 상관없이 블록 매칭 알고리즘을 적용한 실험에 비해 비교적 객체의 움직임을 잘 추적하는 것을 볼 수 있다. 그림 7은 파티클 필터를 이용한 다중 객체의 움직임 환경에서 특정 객체의 움직임을 추적한 실험 결과이다.

그림 7의 실험에서 사용한 영상은 다음의 주소(http://people.csail.mit.edu/jamesm/index.php)에서 이용 가능하다. 그림 7의 실험 결과로부터 다중 객체의 움직임 환경에서 특정 객체의 움직임을 잘 추적하는 것을 볼 수 있다. 그러나 그림 8과 같이 움직임을 추적하는 객체가 다른 객체와 겹쳐질 경우, 추적하고 있는 객체가 아닌 다른 객체를 추적하는 문제점을 나타낸다.결론 및 향후 과제

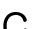
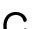
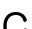
본 고를 통해서 대표적인 추적 필터인 칼만 필터와 달리 사후 분포를 해석적으로 구하는 것이 아니라 상태 변수를 대표할 수 있는 다수의 파티클과 각 파티클이 가지는 가중치를 통하여 표현한 파티클 필터를 사용한 특정 객체의 움직임 추적 방법에 대하여 살펴보았다. 영상의 압축에 사용하는 움직임 예측 방법 중 하나인 블록 매칭 알고리즘의 경우 단일 객체의 움직임 추적에는 적합한 알고리즘이지만 다중 객체의 움직임 환경에서 특정 객체의 움직임을 추적하는 것이 불가능하다는 단점이 있다. 따라서 이러한 문제점에 대한 대안으로 파티클 필터를 사용하여 객체의 움직임 추적을 실험하였다. 실험 결과 블록 매칭 알고리즘과 비교했을 때 단일 객체의 움직임 추적에서 더욱 정확한 추적 결과를 보여주었다. 또한 다중 객체의 움직임 환경에서 특정 객체의 움직임 추적에서 만족할 만한 결과를 얻을 수 있었다. 그러나 움직임을 추적하는 객체가 다른 객체와 겹쳐질 경우, 추적하고 있는 객체가 아닌 다른 객체를 추적하는 문제점이 발견되었다.

향후 연구는 다음과 같은 점을 고려하여 진행해 나갈 예정이다. 첫째, 파티클 필터의 초기값을 마우스 입력이 아닌 움직이는 객체를 자동으로 검출하여 추적하는 방법에 대해 연구할 것이다. 둘째, 다중 객체의 움직임 환경에서 움직임을 추적하는 객체가 다른 객체와 겹쳐질 경우, 추적하고 있는 객체가 아닌 다른 객체를 추적하는 문제점 해결 방법에 대해 연구할 것이다. 셋째, 파티클 필터를 이용한 다중 객체의 움직임 추적에 대해 연구할 것이다.

이러한 과정을 통하여 본 고에서 제안한 알고리즘의 성능을 평가하고, 수정이 필요한 부분을 보완하여 영상을 이용한 객체의 움직임 추적에 더욱 적합한 알고리즘을 만들어 낼 수 있을 것이다.

<본 내용은 심귀보, 김형복 연구 '한국지능시스템학회논문지 21권 제1호'에 게재된 논문을 바탕으로 정리한 것입니다.>